|
# include <iostream.h>
# include <stdlib.h>
# include <conio.h>
# define MAX_VERTICES 10
# define MAX_EDGES 15
class Vertex
{
public:
int label;
public:
Vertex( ) { }
~Vertex( ) { }
void SetVertex(const int);
};
class Edge
{
public:
int weight;
Vertex V1;
Vertex V2;
public:
Edge( ) { }
~Edge( ) { }
void SetEdge(const Vertex,const Vertex,const int);
};
void Vertex::SetVertex(const int _label)
{
label=_label;
}
void Edge::SetEdge(const Vertex _V1,const Vertex _V2,const int _weight)
{
V1=_V1;
V2=_V2;
weight=_weight;
}
int main( )
{
clrscr( );
Sample Input
************
Vertices , Edges
۶ , ۱۰
Vertex_1 , Vertex_2
۳۲۰ , ۱۰۰
۱۷۰ , ۲۰۰
۳۲۰ , ۲۵۰
۴۷۰ , ۲۰۰
۲۲۰ , ۴۰۰
۴۲۰ , ۴۰۰
Vertxe_1 —-> Vertex_2 , Weight
۱ —-> 2 , 6
۱ —-> 4 , 5
۱ —-> 3 , 1
۲ —-> 3 , 5
۲ —-> 5 , 3
۳ —-> 5 , 6
۳ —-> 6 , 4
۳ —-> 4 , 5
۴ —-> 5 , 2
۵ —-> 5 , 6
Answer : 15
int vertices=0;
int edges=0;
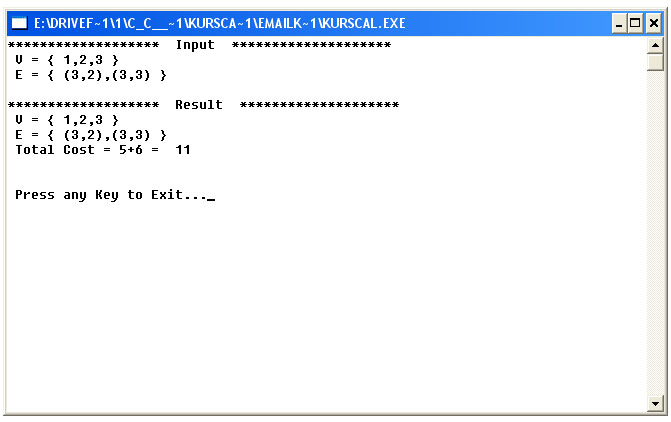
cout<<“**** Input ***”<<endl;
cout<<“Enter the Total Number of Vertices (1-10) = “;
cin>>vertices;
vertices=((vertices<1)?1:vertices);
vertices=((vertices>10)?10:vertices);
cout<<“Enter the Total Number of Edges (1-15) = “;
cin>>edges;
edges=((edges<0)?0:edges);
edges=((edges>15)?15:edges);
Vertex V[MAX_VERTICES];
Edge E[MAX_EDGES];
for(int count=0;count<vertices;count++)
V[count].SetVertex(count);
int v1;
int v2;
int weight;
cout<<“\n ** Edges and their Weights * “<<endl;
for(count=0;count<edges;count++)
{
cout<<” ———- ———->”;
gotoxy(2,wherey( ));
cin>>v1;
gotoxy(35,(wherey( )-1));
cin>>v2;
gotoxy(17,(wherey( )-1));
cin>>weight;
v1=((v1<1)?1:v1);
v1=((v1>vertices)?vertices:v1);
v2=((v2<1)?1:v2);
v2=((v2>vertices)?vertices:v2);
weight=((weight<=0)?0:weight);
E[count].SetEdge(V[(v1-1)],V[(v2-1)],weight);
}
cout<<endl<<“Press any key to Apply Kruskal’s Algorithm…”;
getch( );
clrscr( );
cout<<“*** Input ****”<<endl;
cout<<” V = { “;
for(count=1;count<vertices;count++)
cout<<count<<“,”;
cout<<count<<” } “<<endl;
cout<<” E = { “;
for(count=0;count<edges;count++)
{
cout<<“(“<<(E[count].V1.label+1)<<“,”<<(E[count].V2.label+1)<<“)”;
if(count<(edges-1))
cout<<“,”;
}
cout<<” } “<<endl<<endl;
for(int i=0;i<edges;i++)
{
for(int j=0;j<(edges-1);j++)
{
if(E[j].weight>=E[(j+1)].weight)
{
Edge Temp;
Temp=E[j];
E[j]=E[(j+1)];
E[(j+1)]=Temp;
}
}
}
int e_count=0;
int cycle_flag=0;
Edge _E[MAX_EDGES];
int mst[MAX_VERTICES][MAX_VERTICES]={0};
for(i=0;i<=vertices;i++)
{
mst[i][0]=i;
for(int j=1;j<vertices;j++)
mst[i][j]=-1;
}
for(count=0;count<edges;count++)
{
cycle_flag=0;
for(i=1;i<vertices;i++)
{
if(mst[E[count].V1.label][i]==E[count].V2.label ||
mst[E[count].V2.label][i]==E[count].V1.label)
cycle_flag=1;
}
if(!cycle_flag)
{
_E[e_count]=E[count];
e_count++;
for(i=1;i<vertices;i++)
{
if(mst[E[count].V1.label][i]==E[count].V2.label)
break;
if(mst[E[count].V1.label][i]==-1)
{
mst[E[count].V1.label][i]=E[count].V2.label;
break;
}
}
for(i=1;i<vertices;i++)
{
if(mst[E[count].V2.label][i]==E[count].V1.label)
break;
if(mst[E[count].V2.label][i]==-1)
{
mst[E[count].V2.label][i]=E[count].V1.label;
break;
}
}
for(i=0;i<vertices;i++)
{
for(int j=0;j<vertices;j++)
{
for(int k=1;k<vertices;k++)
{
if(mst[j][k]!=-1)
{
for(int l=1;l<vertices;l++)
{
if(mst[mst[j][k]][l]!=-1)
{
for(int m=0;m<vertices;m++)
{
if(mst[mst[j][k]][l]==mst[j][m])
break;
if(mst[j][m]==-1)
{
mst[j][m]=mst[mst[j][k]][l];
break;
}
|


 مربوط به احداث خط مستقیم بین شهرهای
مربوط به احداث خط مستقیم بین شهرهای  شبکه را طوری طراحی کنیم که مجموع هزینههای ساخت به کمترین مقدار خود برسد. با در نظر گرفتن هر شهر به عنوان یک راس از گراف وزن دار با وزنهای
شبکه را طوری طراحی کنیم که مجموع هزینههای ساخت به کمترین مقدار خود برسد. با در نظر گرفتن هر شهر به عنوان یک راس از گراف وزن دار با وزنهای 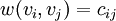 مسئله به یافتن یک زیر گراف فراگیر همبند با کمترین وزن در یک گراف منجر میشود.
مسئله به یافتن یک زیر گراف فراگیر همبند با کمترین وزن در یک گراف منجر میشود.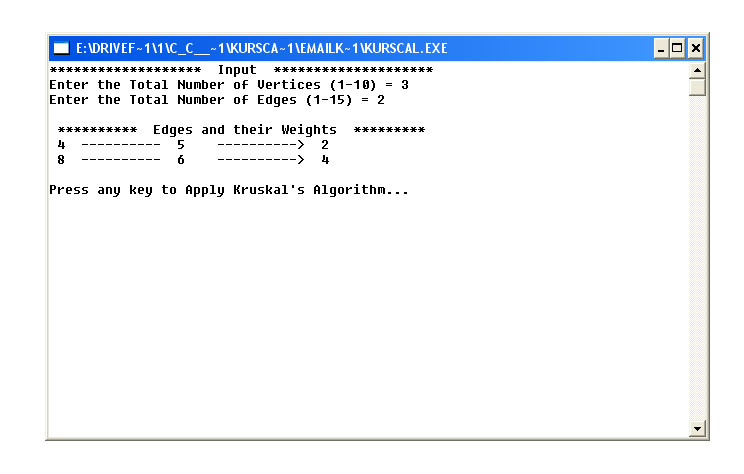

 :
:

دیدگاهتان را بنویسید